Rules
- A 'group' consists of connected stones of one color. A single stone is a group by definition. The adjacent vacant cells of a group are called its 'liberties'. A group that has at least one liberty is called a 'live' group. A group without liberties is called 'dead' because it can no longer influence the outcome of a game.
 |
There are two players, Black and White. Both have a sufficient number of stones in their color. The game starts on an empty board. White moves first. Moving is compulsory. On his turn a player must either:
|
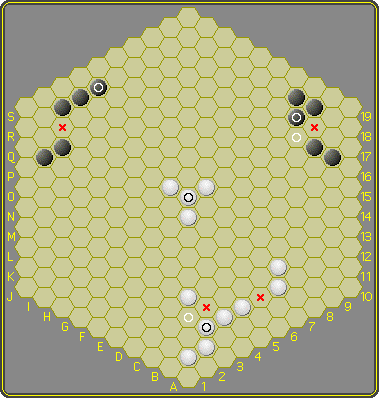
A short clarification: top-left black has grown one group (the marked stone). Now he may not grow the leftmost group at the cell marked 'X', because the other group would have two new adjacent stones.
Top-right a similar situation, but now black may still grow the rightmost group at the cell marked with a white spot. He connects to an already grown group, but only the newly grown stones touch and no original group has grown more than one stone.
In the center, the marked white stone connects three groups, turning the 'local score' from -3 to +2 (see: object). No further stones may be added to the resulting group in this turn, and of course he now may only grow one stone at it in his next turn.
At the bottom white has grown the marked stone. Now cells marked 'X' are off limits, and the cell marked with a white dot is still optional for growth.
Note: a player is free to choose the order of growth. On rare occasions a group with only one or a few liberties, may not be allowed to grow, because a stone at any one of its liberties would also grow another group that did already grow in the same turn.
Object
The game ends by one player's resignation or when the board is full.
The winner is now the player with the highest score. A player's score is counted as the number of stones he has placed on the board minus an even number of points (P) for every separate group. The applet allows P to be set from 2-12.
Note: This parameter is central to the theme. The applet allows P to be set at 2, 4 ... 12, because these would seem to give the most interesting play. The nature of the game's strategy changes with the choice of the parameter.
The dilemma
The dilemma is, to a substantial degree, how long to create new groups and when to start growing them. More groups are needed to be able to grow faster in the subsequent turns, but the more groups there are, the more tempting it becomes to be the first to grow, because of the initiative the combination of several growing moves allows. Moreover every new group starts at -1, and too many groups may eventually affect the score in a negative way, deep in the endgame.
Within that dilemma, there's a second one concerning black's prerogative. Without it, white would have the advantage. With it, black has an advantage which he would like to cash in as late as possible in the opening stage. However, the longer he waits, the greater the chance that white will grow, therewith preventing black to cash in by returning the 'first move advantage' in exchange for a headstart in growing.
After this 'growing intermezzo', both players will likely return to creating new groups for a while, till the main dilemma kicks in.
Strategy
Barring the exchange or cashing in of black's prerogative, the concensus for starting to grow at the moment hovers upward from the square root of half the number of cells of the board. Base-10 that's upwards from move eleven, although tactical developments may induce earlier growth.
The opening stones should be placed so as to be able to secure as much territory for potential growth as possible. Having the edge of the board in the back is a good means for that, so 'go-like' play along the edges seems natural. Keeping groups disconnected is also crucial in this stage, to ensure prolongued growth potential.
Towards in the endgame, when growth potential has severely diminished, opportunities may arise to get points by cutting the opponent's groups or connecting one's own.
Invasions: It may be favorable to start a new group within the 'opponent's territory', if it can grow enough to outgrow it's negative starting value. That of course depends on the value of P: the higher it is set, the more stones are needed to create a group that contributes positively to the score, and the more difficult invasions will become. It may be very unfavorable to be forced to start a new group because the growing options have run out. This is no exception in and endgame, so keeping growing options is important in that stage.
Character
Symple's character is that of a pure strategical game, where small tactical advantages must accumulate on a sound positional strategy. In the endgame however, tactical issues regarding the connection of groups or the forced creation of new ones, will sharply increase the tension and drama in balanced games.
Counting
The applet continually counts the number stones minus P points for every seperate group for both players. When the board is full, this constitutes the score.
Hexagonal hexboards have an odd number of cells, so the endscore cannot be equal.
How I invented ... Symple
HexSymple © MindSports and Benedikt Rosenau
