 | The Set A TriAx piece consists of three dicubes (1*1*2), one in a north-south direction, one in an east-west direction and one in an up-down direction. The set of 28 pieces consists of all different ways a piece can be formed this way. Two pieces are considered to be equal if by spatial rotations they can exactly be mapped onto each other, with the dicubes in corresponding positions. Compare pieces 27 and 28. These are: (I) unequal if we take the relative positions of the composing dicubes into account. (II) equal if we only consider the spaced occupied by these pieces. Since each piece consists of 6 unit-cubes, the set comprises 168 cubes. Thus, spacial blocks with a volume of 168 cubes may be filled with it. Because a TriAx-piece is never flat, edges of such blocks will measure at least 2 unit-edges. |
Block solutions
The prime factors of 168 are 2 * 2 * 2 * 3 * 7. Thus the following blocks may be tried:
| a) 2*12*7 | b) 2*6*14 | c) 4*6*7 | d) 8*3*7 |
| e) 4*3*14 | f) 2*2*42 | g) 2*4*21 | h) 2*3*28 |
i) 2 blocks of 2*6*7
j) 2 blocks of 3*4*7
k) 4 blocks resp. 2*3*4 + 3*3*4 + 4*3*4 + 5*3*4
l) 4 blocks resp. 2 of 3*3*4 + 2 of 4*3*4
j) 2 blocks of 3*4*7
k) 4 blocks resp. 2*3*4 + 3*3*4 + 4*3*4 + 5*3*4
l) 4 blocks resp. 2 of 3*3*4 + 2 of 4*3*4
Solutions of k) render, by repositioning, solutions of c), d), e) en j). A solution of i) likewise renders solutions of a) and b).
With the exception of f) and g), solutions for these possibilities have been found. Some 'block-solutions' are impossible because of the following theorem, the proof of which is omitted here:
A block of arbitrary size with edges x, y and z units, cannot be filled with TriAx-pieces if x*y*z is not divisible by 12.
This means that there are no solutions for, for instance, 3 blocks of 2*4*7 or for a block of 2*4*10 and a block of 2*4*11.
A single dicube in particular cannot be triplicated (3*3*6), thus the 'universal' triplication of all piece, by using three triplicated dicubes, does not exist.
Although no solutions have been found for the cases f) and g), theorem 1 does not exclude these. Nevertheless f) seems, by intuition, a hard case.
 | A 4-boxes solution Obviously these four boxes, 2*3*4, 3*3*4, 4*3*4 and 5*3*4 can be rearranged to one in several ways: 14*3*4, 7*6*4 and 7*3*8. |
 |
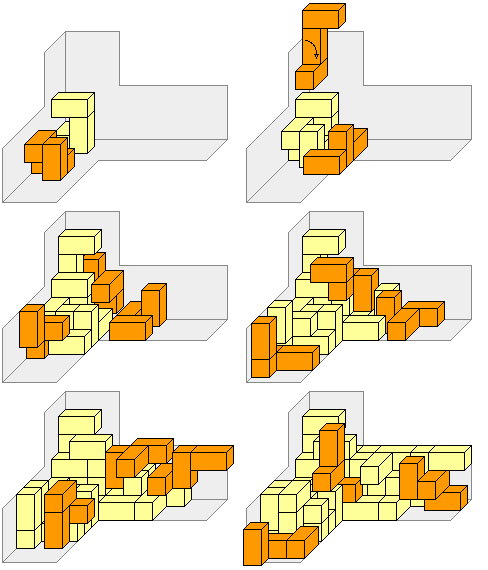  | A triplication of #9 An interesting property of the set is that it allows triplications of any piece with the 27 pieces that are left. This renders essentially 15 new puzzles because 2 of the 28 pieces are unchanched by reflection. The remaining 26 pieces come in pairs and of course solving one of a pair means solving both. Triplications have been found for all pieces! As a consequence of theorem 1, it is not possible to triplicate a di-cube. If it were, all triplications would be solved at once, but a di-cube's volume, 3*3*6, is not divisible by 12. Also, it is not possible to obtain a triplication by dividing and rearranging another triplication: Each triplication is a puzzle in itself. This property appears to be unique for the TriAx. |
TriAx © MindSports.
