Page 29 of 47
KnightVision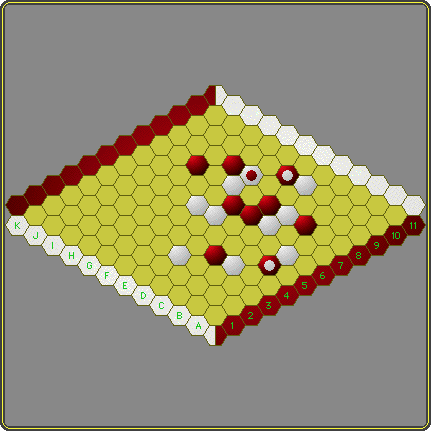 |
|
Still January, still a full lockdown, still waiting for the sun and a covid shot. I wasn't done yet, apparently. We got sightlines on a hexboard, orthogonal or diagonal, both pretty clear. Less clear are knightlines, especially on a hex board. But two cells at a 'knight's distance', that's pretty clear: the cells D2, D3, B4 and C4 are all at a knight's distance from the bottom cell A1. I was still thinking about the Tumbleweed protocol and figured that instead of placing 'in sight' of at least one friendly piece, you might choose to have it placed at a knight's distance of at least one friendly piece. Analogous to Cannons & Bullets you can then reward placement at a knight's distance of three or more friendly pieces with a 'bullet' for the placed piece, one that can be shot rookwise as in the parent game. I realised that I could call the pieces 'knights' and the bullets 'axes' and have a hexhex territory game with a slightly different placement protocol. But that would not be all that interesting, not to mention appalingly lazy. So I considered a connection goal, like Hex. Now here's the thing: with single placement at a mandatory knight's distance of at least one friendly piece you can get a long way. In fact it's hard to imagine that a player could be out of possible cells to place a piece but of course it's easy to make an example of precisely that situation. In such a case a player could be forced to forfeit his turn and the board would fill up and someone would win. A kind of Handicap-Hex that I wouldn't discard as uninteresting. But ... I'm not in the habit of discarding simple ideas and there's problably a lot of hex strategy involved in the described game as is, but in this case I' decided to spice it up tactically. So I maintained the condition for getting an 'axe', that is: placing a double at a knight's distance of at least three friendly pieces and calling the top piece the axe. The owner then has the option of throwing the axe as the bullets in Cannons & Bullets, moving over vacant cells and friendly pieces and landing on a vacant cell or capturing the first opponent's piece that it encounters. The goal is now of course taken from Hex. The game is finite and decisive. Enschede, January 2021 christian freeling |
